Predicting Breast Cancer Treatment Responses with Mathematical Models

Can mathematics help physicians make better decisions for cancer patients? A new study led by professor Tom Yankeelov, Director of the Center for Computational Oncology at the Oden Institute for Computational Engineering and Sciences, suggests the answer is, “yes.”

The team developed a biology-based mathematical model capable of predicting how breast cancer responds to neoadjuvant chemotherapy, which is given before surgery to shrink tumors. By using magnetic resonance imaging (MRI) scans acquired at the beginning of treatment and just three weeks later, the model accurately forecasted tumor changes after nine weeks.

“We are trying to develop mathematical models that allow you to predict how a tumor grows in space and time and then use that information to optimize the way patients are treated,” explained Yankeelov, who is also a professor of Biomedical Engineering, Diagnostic Medicine, and Oncology at The University of Texas at Austin.

Unlike machine learning and other statistical approaches that rely on massive datasets and population averages, the Oden Institute team’s models are rooted in biology itself. They incorporate the known physical processes of cancer: how tumor cells grow, move, interact with surrounding tissues, and respond to therapy. These processes are captured mathematically through partial differential equations (a type of equation that describes changes in space and time).

This patient-specific approach means the model doesn’t just look at what worked for most people. Instead, it is tailored to the individual. “If you want to improve how an individual will respond to treatment, then you have to be able to predict how a given intervention will work on that individual,” Yankeelov said.

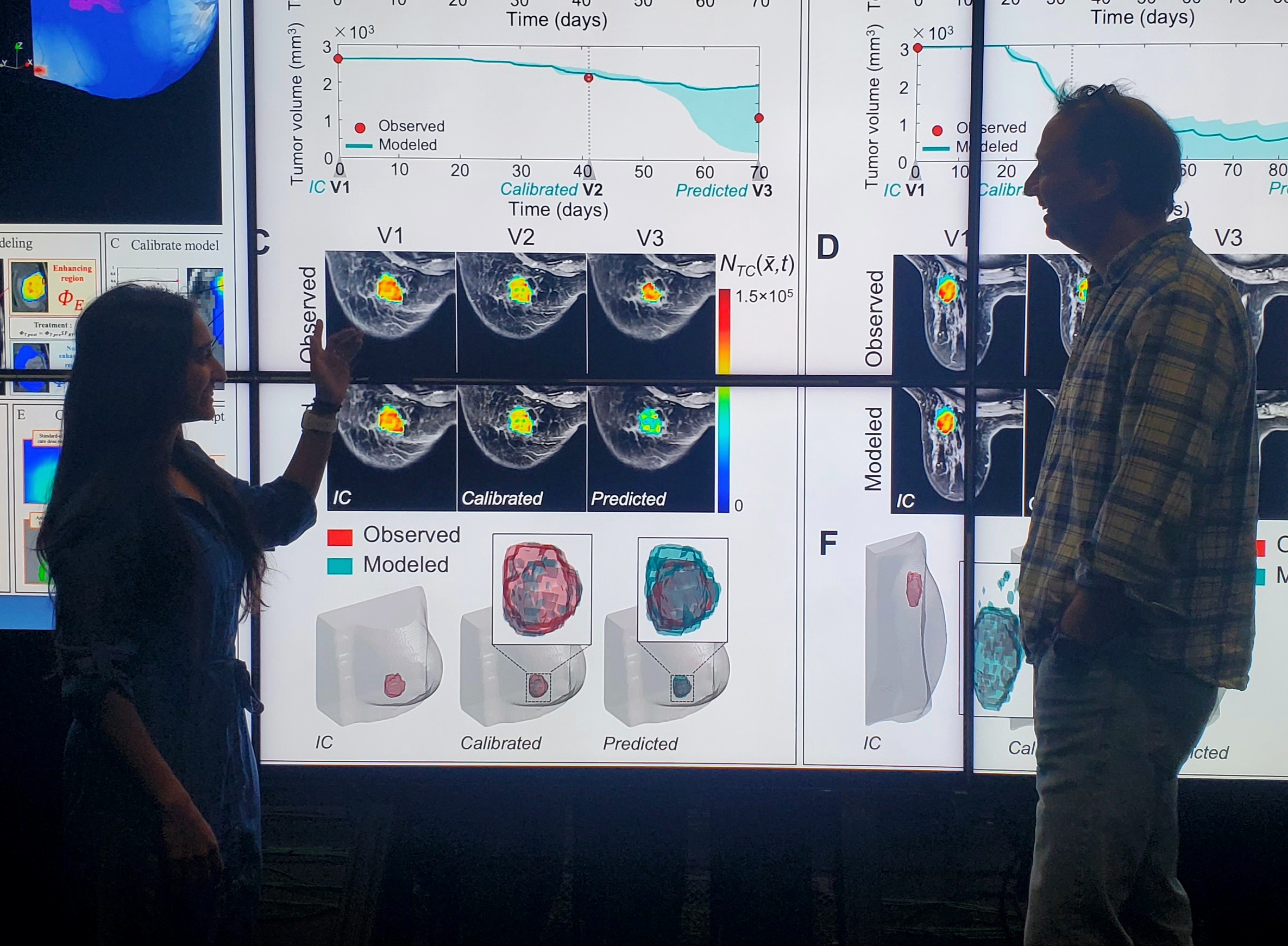
To validate their work, the team analyzed data from 91 breast cancer patients across 10 clinical trial sites, covering three different subtypes of breast cancer. This diversity of data was critical to testing the robustness of the model. “When you get data from 10 different clinical sites, there can be a fair amount of variation in the quality and quantity of data,” Yankeelov explained. “So, if your mathematical model is able to make accurate predictions on data with that degree of variability, then you start to think that you are on to something that captures key features of tumors and what causes them to grow or respond to therapy.”

A key collaborabor on the study, Chengyue Wu, an assistant professor in the Department of Imaging Physics at UT's MD Anderson Cancer Center, noted the long path that brought the team to this point. “It’s quite a journey to develop the mathematical model for breast cancer treatment response and gradually validate it through multiple studies. We started the proof-of-principal development in a small cohort of about 10 cases, then we’ve been refining it and applied it to a single-institutional large cohort. Now we are able to validate its generalizability in the multi-institutional I-SPY2 cohort. It is super exciting to see the continuous growth of evidence and confidence for our model’s ability to make real-world impact in breast cancer care.” Wu is also an Oden Institute alumna.

The results were striking as the model achieved a 0.94 correlation between predicted and observed changes in tumor cellularity and a 0.90 correlation for tumor volume. These results demonstrate that the model not only works in theory, but can accurately forecast outcomes in real-world, diverse patient populations.

Graduate research assistant Reshmi Patel, the paper’s first author, played the central role in the project. For her, the most rewarding part was seeing the model’s predictive power in action. “The first time I calibrated the mathematical model to an individual patient’s MRI data and ran it forward to make an accurate prediction nine weeks in the future, it felt like a little bit of magic,” Patel recalled.

Her day-to-day work involved coding, analyzing MRI data, and debugging the models. But beyond the technical details, Patel was motivated by the potential impact. “I am very grateful to have the opportunity to work on a research project that could—in some small way—contribute to better patient outcomes down the line,” she said.

In the near future, Yankeelov and his team envision this modeling framework being used as a decision-support tool for oncologists. After just a few treatment cycles, the model could help doctors decide whether to continue with the current plan or adjust it—tailoring care to each patient rather than relying on population averages.

Patel echoed this point: “After a patient receives three chemotherapy cycles, we could calibrate a mathematical model with patient-specific MRI data and make predictions at the end of treatment for a range of treatment schedules. We could then provide information about which schedule best balances efficacy and toxicity.”

The next step, Yankeelov says, is to test the model in prospective clinical trials where predictions actively guide treatment strategies. While there is enthusiasm among many clinical collaborators, introducing mathematical models into patient care comes with challenges. “We have some absolutely awesome clinical collaborators, but not everyone is on board with the idea of using a math model to guide treatment,” he admitted.

Still, publication of the study in Clinical Cancer Research, indicates the growing recognition of mathematical modeling in oncology.